The Schelling Segregation Model Back to simulation
Classification tags: social science, grid space model, fixed-increment time progression.
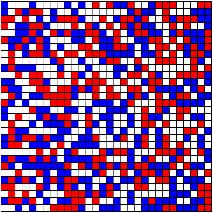
Classification tags: social science, grid space model, fixed-increment time progression.

Thomas C. Schelling, who is a co-recipient of the 2005 Nobel Prize in Economics, published a paper proposing a theory about the persistence of racial or ethnic segregation despite an environment of growing tolerance ("Dynamic Models of Segregation", Journal of Mathematical Sociology 1, 1971, 143-186.). He suggested that even if individuals tolerate racial diversity, if they also remain uneasy about being a minority in the locality, segregation will still be the equilibrium situation.
Schelling placed pennies and dimes on a chess board and moved them around according to various rules. He interpreted the board as a city, with each square of the board representing a house or a lot. He interpreted the pennies and dimes as residents representing any two groups in society, such as two different races of people, boys and girls, smokers and non-smokers, etc. The neighborhood of a resident occupying any location on the board consisted of the squares adjacent to this location. Thus, interior (non-edge) residents could have up to eight neighbors, non-corner edge residents could have a maximum of five neighbors, and corner edge residents could have a maximum of three neighbors. Rules could be specified that determined whether a particular resident was content in her current location. If she was not, she would try to move to another location on the board, or possibly just exit the board entirely. As can be expected, Schelling found that the board quickly evolved into a strongly segregated location pattern if the residents' "contentness rules" were specified so that segregation was heavily favored. Surprisingly, however, he also found that initially integrated boards tipped into full segregation even if the residents' contentness rules expressed only a mild preference for having neighbors of their own group.
The conceptual model for studying segregation as a social phenomena describes the behavior of residents as members of some group, being either content or uncontent with their neighborhood, and moving to another place as a consequence of being uncontent.
Residential segregation involves residents living at some address as members of some group and their neighborhoods as spatial structures. Consequently, potentially relevant object types are:
Potentially relevant types of events are:
Both object types and event types, with their participation associations, can be visually described in a UML class diagram, as shown below.
| ON (event type) | DO (event routine) |
| Periodical neighborhood check | If there is not a sufficient number of neighbors of the same group, then search a place with a sufficient number of neighbors of the same group and, if found, move to it, otherwise move out of the neighborhood. |
| Move to a destination | Update the resident's address. |
Research question: what is the degree of segregation obtained with reasonably tolerant residents?
We can make the following simplifications as design choices:
Each resident has a neighborhood consisting of the 8 adjacent cells surrounding it, both vertically/horizontally (N/E/S/W) and diagonally (NE/SE/SW/NW).
The OESjs simulation framework provides two forms of grid spaces: (1) a simple integer grid, where a grid cell has an integer value that can, for instance, represent the group of the resident at this location, and (2) an object grid, where a grid cell is a special type of object such that one can define properties for it and associate it with a set of objects that are positioned on this grid cell. Obviously, choosing an integer grid as the space model of a simulation implies limitations on the information that can be represented per grid cell, but allows larger grid spaces compared to object grids because of its smaller memory footprint.
In the SchellingSegregationModel-1, an integer grid has been chosen as the space model such that the
integer value of a grid cell being zero represents an empty space location, while a value of greater than zero
represents the number of the group to which the resident located on that cell belongs. Since residents are
not modeled explicitly, as individual objects, but rather implicitly, as grid cell values, in this design,
no object type Resident, but only an object type GroupOfResidents is defined for
being able to assign different tolerance levels to different groups of residents.
As a design choice, we abstract away from the real-world events described in the conceptual model, based on the assumption that their temporal dependency structure is not relevant for capturing the dynamics of the segregation process. Instead of modeling events as the basis of driving the simulation with a next-event time progression loop, the design relies on an abstract discrete time model and on implicit time step events driving the simulation with a fixed-increment time progression loop. Consequently, the information design model does not contain any event types.
| ON (event type) | DO (event routine) |
| Each simulation time step |
Pick a resident r that is uncontent and search for a free cell where r would be content IF there is such a cell THEN move r to this cell ELSE remove r from the grid Re-evaluate the contentness of all residents affected by this change |